Number System:

A number system is a way of representing and expressing numbers using a set of symbols or digits consistently. It provides a framework for performing mathematical operations like addition, subtraction, multiplication, and division.

A digital number system is a way of representing numbers so that digital devices (like computers) can understand, store, and process them. The most commonly used digital number system is the binary system, which works with just 0 and 1.

Types of Number Systems:

1. Decimal number system: The decimal number system, also known as the base-10 system, is the most commonly used number system in our daily life. It uses ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each digit in a number has a place value, which is based on powers of 10 depending on its position.

2. Binary Number System: The binary number system is a number system that uses only two digits: 0 and 1. It is also called the base-2 system. Each digit in a binary number is called a bit. Computers and digital devices use the binary system to store and process data because they work with two states: ON (1) and OFF (0).

3. Octal number: The octal number system is a number system that uses eight digits: 0 to 7. It is also called the base-8 system. Each digit in an octal number has a place value based on powers of 8. The octal system is often used in computer programming as a shorter way to represent binary numbers.

4. Hexadecimal number system: The hexadecimal number system is a number system that uses sixteen symbols: the digits 0 to 9 and the letters A to F. It is also called the base-16 system. In this system, A stands for 10, B for 11, C for 12, D for 13, E for 14, and F for 15. Hexadecimal is commonly used in computers and digital systems because it makes large binary numbers easier to read and understand.

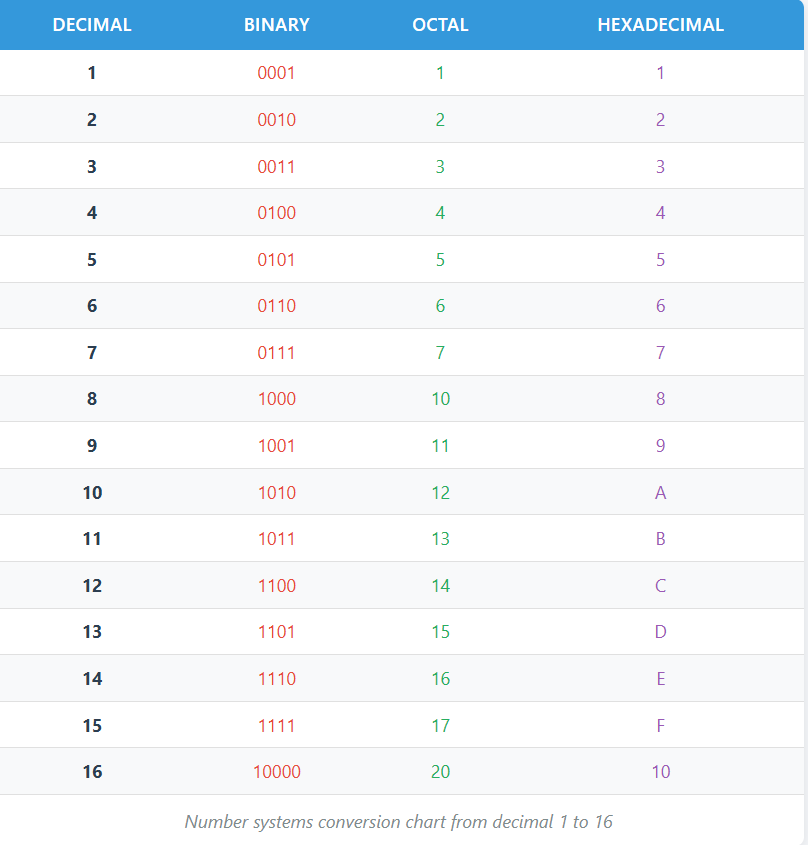
Number system table:

Number conversion:

Decimal to binary conversion 

Steps

1. Divide the decimal number by 2.
2. Write down the remainder (0 or 1).
3. Divide the quotient again by 2 and write the next remainder.
4. Repeat this process until the quotient becomes 0.
5. Read the remainders in reverse order (from bottom to top). This is the binary number.

   (i) Convert (52)10 into binary.

Decimal to Binary converter 

Steps to Convert Binary to Decimal:

• Write down the binary number.
• Start from the rightmost digit and assign powers of 2 starting from 0.
• Multiply each binary digit by 2 raised to the power of its position.
• Add all the results from step 3.
• The final sum is the decimal equivalent of the binary number.

Binary to Octal conversion:-

• For conversion from binary to octal, the binary numbers are divided into groups of 3 bits each, starting at the binary point and proceeding towards left and right.

Binary to Hexadecimal conversion:-

• For converting a binary to a hexadecimal number, the binary number starting from the binary point, groups of 4 bits each, on either side of the binary point.

Dicimal to octal Conversion:

• To convert a decimal whole number to octal, divide the number by 8 again and again until the quotient becomes 0.
• To convert a decimal fraction to octal, multiply the fraction by 8 again and again until the result becomes 0 or until you get the required number of decimal places.

Decimal to Hexadecimal Conversion:

• The decimal to hexadecimal conversion is the same as the octal.

octal to binary Conversion

• To convert a given octal number to binary, replace each octal digit by its 3-bit binary equivalent.

Octal to decimal conversion:

• To convert an octal number to a decimal number, multiply each digit in the octal number by the weight of its position and add all the product terms.

Hexadecimal to binary conversion:

• For conversion of hexadecimal to binary, replace a hexadecimal digit with its 4-bit binary group.

Hexadecimal to decimal conversion:-

• For conversion of hexadecimal to decimal, multiply each digit in the hexadecimal number by its position
  weight and add all those product terms.

Hexadecimal to Octal conversion:-

• For conversion of hexadecimal to octal, first convert the given hexadecimal number to binary and then binary number to octal.

Complement’s.

Complements are used in digital computers for simplifying the subtraction operation and for logical manipulations. There are two types of compliments For each base-r system:

1) the r’s complement
2) the (r-1)’s complement

1) the r’s complement: 

Given a positive number N in base r with an integer part of n digits, the r’s complement of N is defined as

     rn –N          for  N does not equal zero 
     0             for  N  equal zero