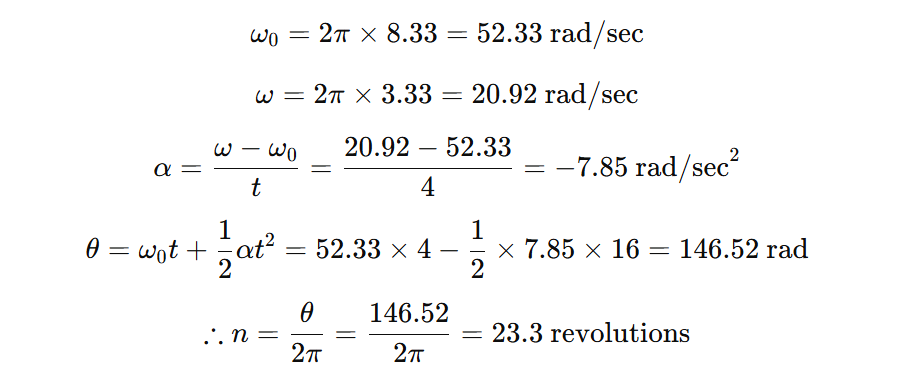Rotational dynamics
In engineering physics, rotational dynamics is the branch of mechanics that studies the motion of objects that rotate or spin about an axis, and the forces and torques that cause or change this motion
Translation Motion And Rotational Motion: A body is said to be in translation motion if each particle of it has equal linear displacement in an equal interval of time. Similarly, a rigid body is said to be in rotational motion if each particle of it has the same angular displacement in an equal interval of time
Note!
In case of rotational motion, all particles have different linear displacement, linear velocity, linear acceleration, but the same angular displacement, angular velocity, and angular acceleration.
Rigid Bodies: A body is said to be a rigid body if it does not undergo any changes in shape and volume when an external force is applied to it. The distance between any two particles for such a body will remain the same no matter how large the external forces are applied on it.
Torque or Moment of Torque: The turning effect of force in a body is called Torque. Mathematically, it is defined as the product of force and its perpendicular distance from the axis of rotation. i.e.
τ = r F1
where f₁ is perpendicular to the moment of am(r) and also f₁ is the component of I along the axis of the rotation.
τ = r F Sinθ
in Vector form:
.τ is a vector quantity whose direction can be determined by the right-hand thumb rule from r and F. It may be clockwise or anti-clockwise. The SI unit of torque is N·m.
Moment of Inertia
The Moment of Inertia of a rigid body about a particular axis of rotation is defined as the sum of the product of the masses of all particles constituting the body and the square of their respective distances from the axis of rotation. From Newton’s second law of motion
F =ma
rF = mar
rF= mr 2α [∵a=rα]
τ = (mr 2) α
Where τ is torque, α is angular acceleration, and mr² is the moment of inertia (I). Thus:
τ=Iα
Hence, the moment of inertia of a rigid body plays the same role as mass in linear motion. I is a scalar quantity, and its unit is kg·m² in the SI system.
Radius of Gyration: The radius of gyration is the distance from the axis of rotation to the point where the total mass of the body is assumed to be concentrated. It may also be defined as the square root of the mean square distance of the various particles of a body from the axis of rotation. It is denoted by k.
The moment of inertia of a body having mass m and radius of gyration k is given by:
I=Mk2
Moment of Inertia for a Body with n Particles
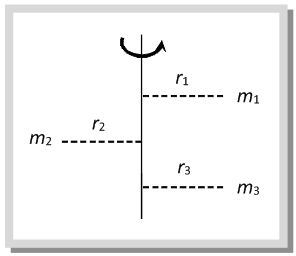
Consider a body consisting of n particles, each of mass m. Let r₁, r₂, r₃, …, rₙ be their perpendicular distances from the axis of rotation. The moment of inertia (I) of the body about the axis of rotation is:

Relation Between Torque and Angular Acceleration

Consider that a rigid body is rotating about an axis YY under the action of a constant torque (T). Also, let the body consist of n particles of masses m₁, m₂, m₃ … mₙ at particular distances r₁, r₂, r₃ … rₙ from the axis of rotation, respectively. Let the torque will produce a constant angular acceleration α in each particle.
Since the particle of mass m₁ follows a circular path of radius r₁, the magnitude of linear (or tangential) acceleration of this particle is:
α1=r1α
The net external force acting on this particle due to this acceleration is:
F1=m1a1=m1r1α
And, the magnitude of the torque acting on this particle due to this force is:
τi=Firi=(miriα)ri=miri2α
So, the total torque acting on the body is
τ=τ1+τ2+τ3+⋯+τn for n particles
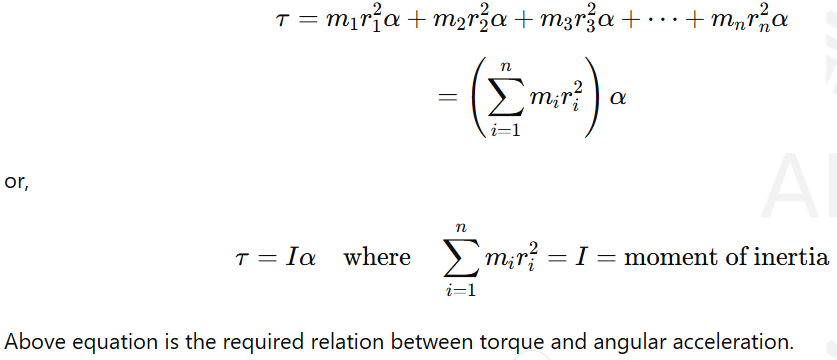
Relation Between Moment of Inertia and Rotational Kinetic Energy
Consider a rigid body rotating with uniform angular velocity ω about a given axis (YY′) as shown in the figure. Let m1, m2, m3,…,mn be the masses of different particles constituting the body. Let r1, r2, r3,…,rn be their respective distances from the axis of rotation.
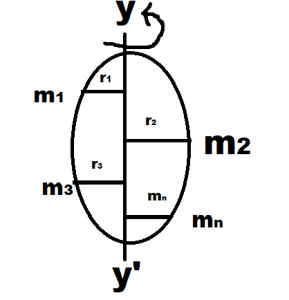
Kinetic Energy of the particle of mass (m₁),
= ½ m₁v₁²
= ½ m₁r₁²ω² [∵ v = rω]
Kinetic Energy of the particle of mass (m₂),
= ½ m₂v₂²
= ½ m₂r₂²ω² and so on.
Rotational Kinetic Energy of the given body (E) is given by:
E = ½ m₁r₁²ω² + ½ m₂r₂²ω² + … + ½ mₙrₙ²ω²
= ½ (Σ mᵢrᵢ²) ω²
E = ½ Iω² ……………….1
Where Σ mᵢrᵢ² = I, moment of Inertia of the body. Equation 1 is the required relation.
Relation Between Angular Momentum and Moment of Inertia:
Consider a rigid body rotating about an axis YY’ as shown in the figure.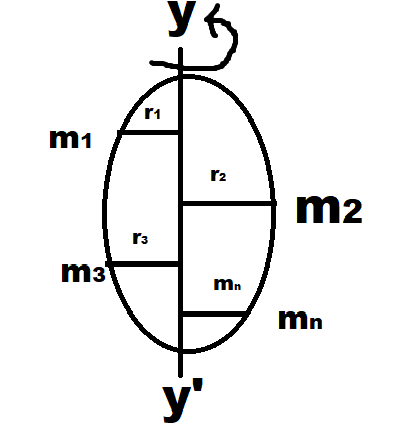 Let m₁, m₂, m₃ … mₙ be the masses of the different particles constituting the body. Let r₁, r₂, r₃ … rₙ be their respective distance from the axis of rotation. Suppose the body be rotating with uniform angular velocity ω about the axis. Although each particle within the body has the same angular velocity ω, their linear velocity will be different.
Let m₁, m₂, m₃ … mₙ be the masses of the different particles constituting the body. Let r₁, r₂, r₃ … rₙ be their respective distance from the axis of rotation. Suppose the body be rotating with uniform angular velocity ω about the axis. Although each particle within the body has the same angular velocity ω, their linear velocity will be different.
Let v₁, v₂, v₃ … vₙ be the linear velocity of the particle of masses m₁, m₂, m₃ … mₙ respectively, then.
v₁ = r₁ω,
v₂ = r₂ω,
vₙ = rₙω
The angular momentum of the mass (m₁) is given by
L₁ = m₁v₁r₁
= m₁r₁ω.r₁
= m₁r₁²ω
Similarly, the angular momentum of the body of masses m₂, m₃ … mₙ can be expressed. Thus, the angular momentum of the body is
L = L₁ + L₂ + L₃ + … + Lₙ
= m₁r₁²ω + m₂r₂²ω + m₃r₃²ω + … + mₙrₙ²ω
= (m₁r₁² + m₂r₂² + m₃r₃² + … + mₙrₙ²)ω
= ( Σ mᵢrᵢ² )ω
∴ L = Iω … …….(1)
where Σ mᵢrᵢ² = I : is the moment of inertia of the body. Equation 1 is the required relation between angular momentum and moment of inertia.
Angular Momentum:
It is defined as the product of linear momentum and perpendicular distance between the body and the axis of rotation. If a body having mass m moves with velocity v at a distance r from the axis of rotation, then
Angular Momentum (L) = Linear Momentum (p) × perpendicular distance between the body and the axis of rotation.
= r×p
= rp sinθ n̂
= rpsin90
= rp
= rmv
= r m (rω)
= mr²ω
∴ L = mωr2
The SI unit of angular momentum is kgm²s⁻¹ and its dimension is [M L² T⁻¹]. It is a vector quantity. L=r×p
Conservation of Angular Momentum:-
If no external torque acts on a system, then the total angular momentum remains conserved or constant. Mathematically,
L = constant { dL/dt = J = dL/dt = 0 }
i.e. Iω = constant
I₁ω₁ = I₂ω₂
Proof:
The torque acting on a body about a given axis of rotation is defined as the rate of change of angular momentum.
i.e. dL/dt = J … (1)
If no external torque acts on a system then,
J = 0
so, dL/dt = 0 … (2)
Integrating equation 2 on both sides, we get
∫ dL/dt = ∫ 0
L = constant
Iω = constant
I₁ω₁ = I₂ω₂
Examples of conservation of angular momentum
- Motion of a planet revolving in an elliptical orbit around the sun
- Ballet Dancer
Moment of Inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length.
Consider a thin rod uniform rod having mass (m) and length (l), which is rotating about an axis passing through its centre and perpendicular to its length, as shown in the figure. Now, to find the moment of inertia, consider the small elements of the rod having mass dm, length dl, at a distance x from the axis YY’. Now,
The moment of Inertia of a small element is given by
dI = dm x² —-………….. (1)
The moment of inertia of the rod is given by
I=∫dI=∫dm⋅x2 ………… (2)
Now,
Mass of length lll of the rod = M
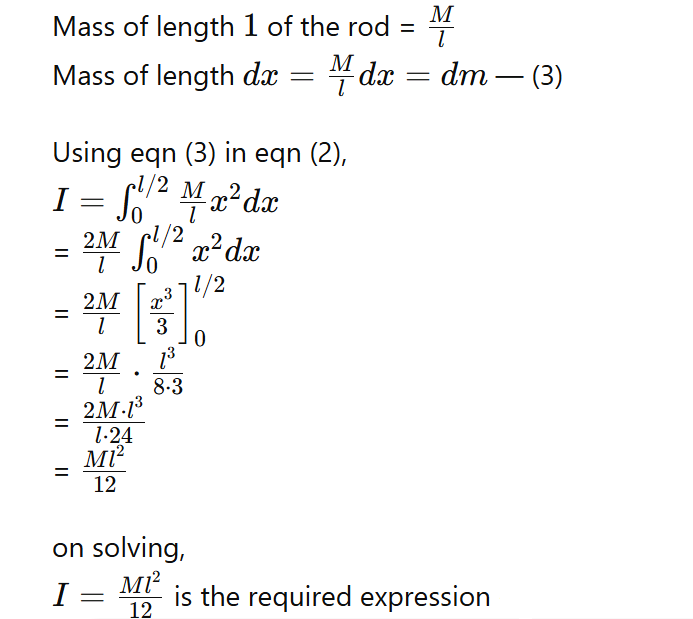
Moment of Inertia of a thin uniform rod about an axis passing through its one end and perpendicular to its length
Let us consider a thin uniform rod having mass M and length l, which is rotating about an axis passing through its one end and perpendicular to its length, as shown in the figure.
Now,
Let us consider the small elements of the rod having mass dm, length dx at a distance x from the axis YY’.
Here, the Moment of Inertia of a small element is given by
dI = dm x² — (1)
The moment of Inertia of a small element of the rod is
I=∫dI = ∫dmx2 …………………(2)
Now
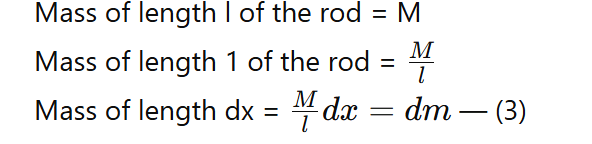
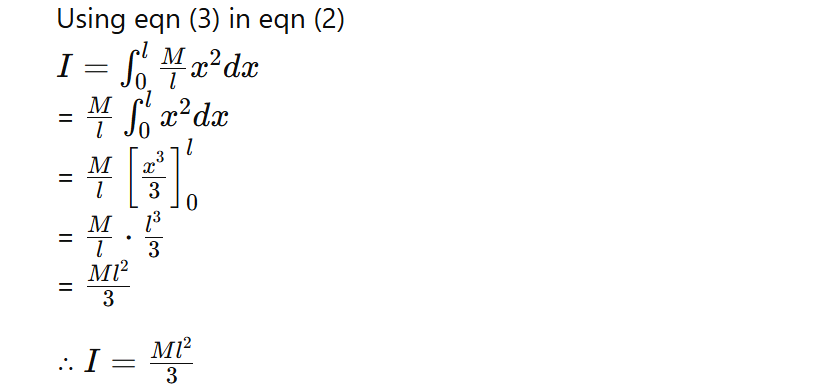
Kinetic Energy of the rotating body
Let us consider a rigid body consisting a number of particles having masses m1,m2,…, mn at a distance r1,r2,…, rn from the axis YY’ as shown in the figure.

Now, the linear velocity of a particle having mass
m1,m2,…,mnm_1, m_2, …, m_nm1,m2,…,mn is given by
v1=r1ω
v2=r2ω
vn = rn ω
The K.E acting on the particle having



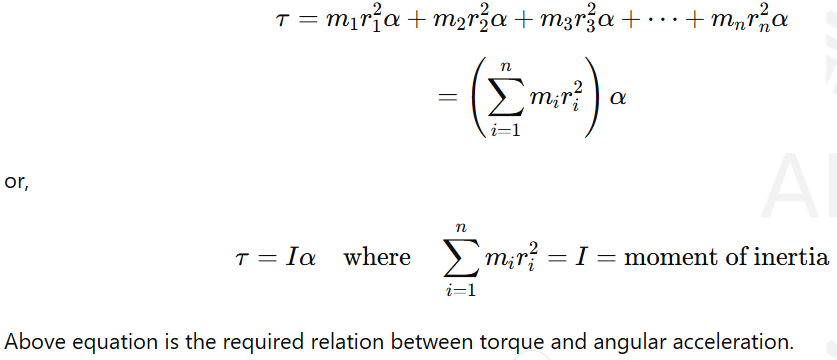

 Let m₁, m₂, m₃ … mₙ be the masses of the different particles constituting the body. Let r₁, r₂, r₃ … rₙ be their respective distance from the axis of rotation. Suppose the body be rotating with uniform angular velocity ω about the axis. Although each particle within the body has the same angular velocity ω, their linear velocity will be different.
Let m₁, m₂, m₃ … mₙ be the masses of the different particles constituting the body. Let r₁, r₂, r₃ … rₙ be their respective distance from the axis of rotation. Suppose the body be rotating with uniform angular velocity ω about the axis. Although each particle within the body has the same angular velocity ω, their linear velocity will be different.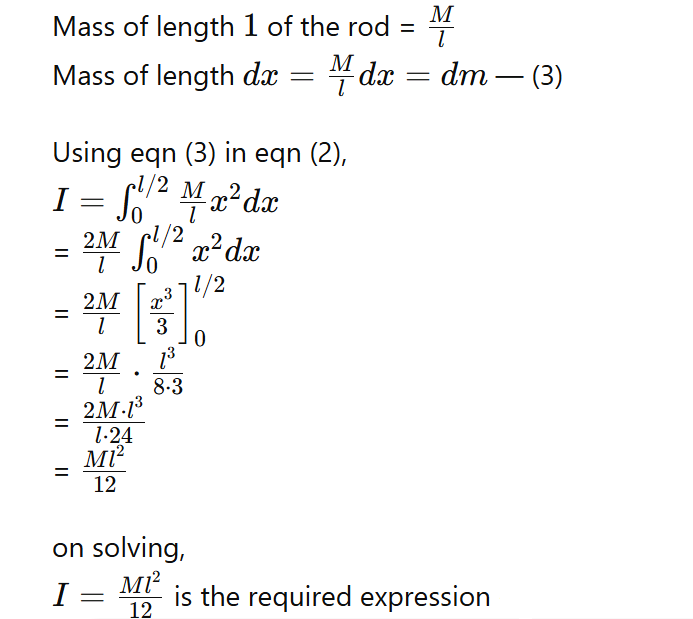
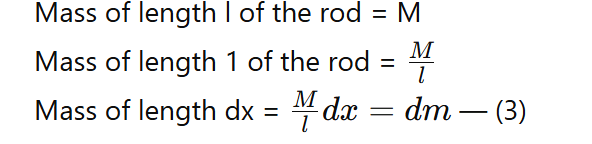
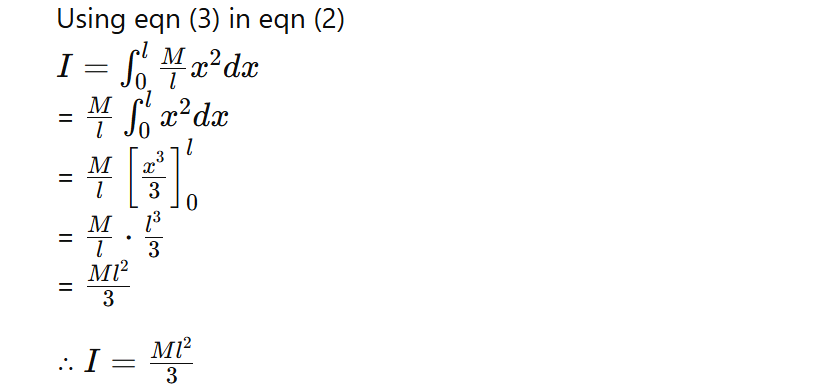

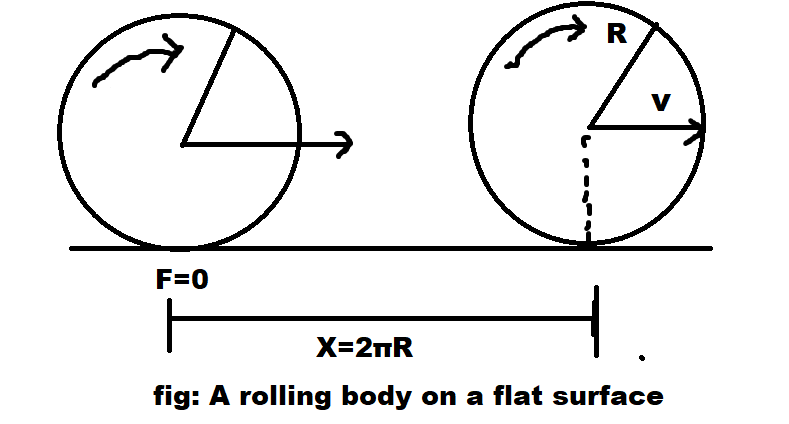


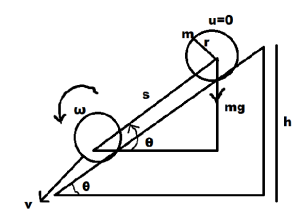
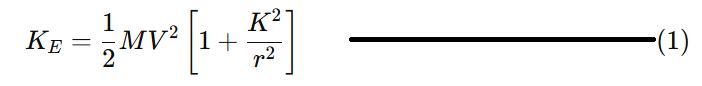
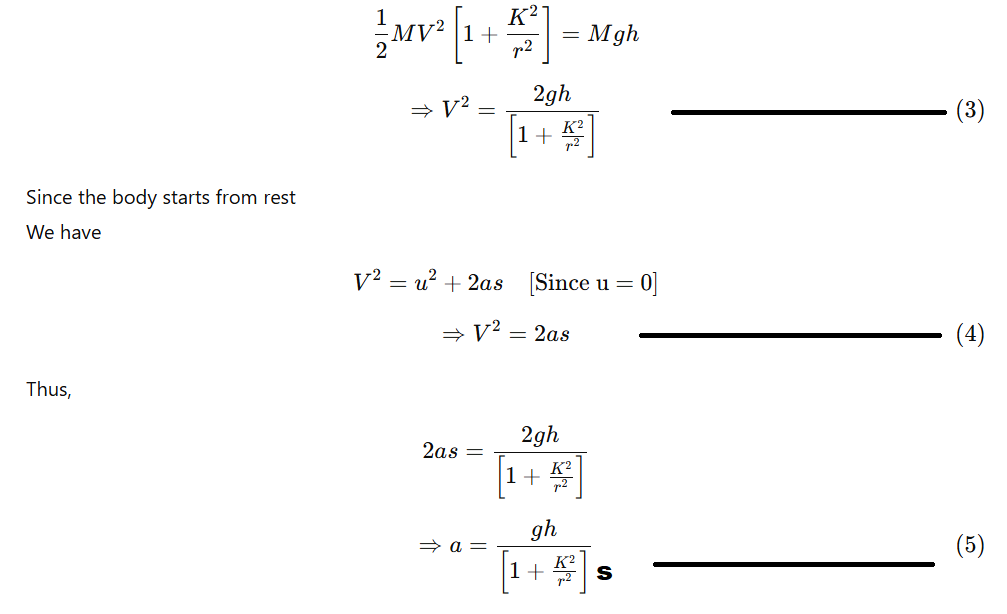 Let S be the length of the inclined plane. Then from ΔABC
Let S be the length of the inclined plane. Then from ΔABC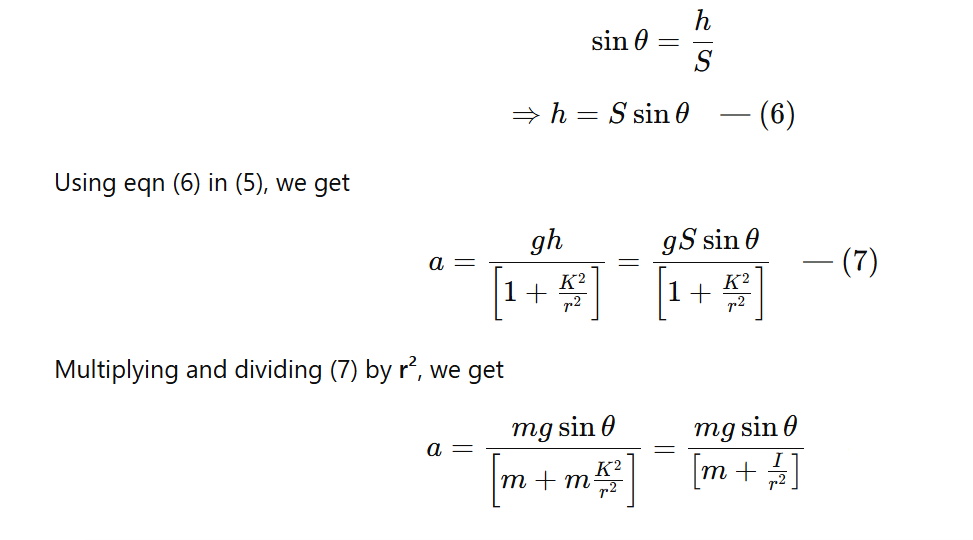
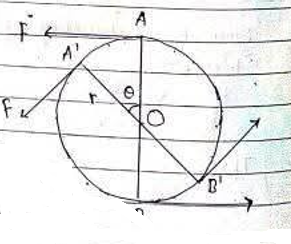 Let us consider a wheel of radius r which is rotating about an axis passing through its centre O′ with angular velocity ω. Let θ be the angular displacement when two equal and opposite forces act at points A and B as shown in fig.
Let us consider a wheel of radius r which is rotating about an axis passing through its centre O′ with angular velocity ω. Let θ be the angular displacement when two equal and opposite forces act at points A and B as shown in fig.