Simple harmonic motion:

A body is said to be in Simple Harmonic Motion, if it moves to and from about its mean position in a straight line such that at any given point its acceleration is directly proportional to the displacement in magnitude but opposite in direction and is directed always towards the mean position. i.e. for SHM,

a ∝ y ( where y is the displacement from mean position)
or, a = – k y ………. 1)

Where, k is proportionality constant. The negative sign indicates that acceleration is directed opposite to the displacement of the object from the mean position. (i.e. acceleration is always directed towards the mean position)

NOTE: If a body is moving in such a way that, with increase in time, it repeats its value of displacement, velocity, acceleration etc. and it can be expressed in the terms of function containing sine or cos, then it is harmonic motion.

Characteristics of Simple Harmonic Motion (SHM):

a) Displacement in SHM: Consider a particle moving in a circular orbit having center at O and radius r with uniform angular velocity ω. Let ‘P’ be the position of the particle at any time t and corresponding angular displacement is θ.

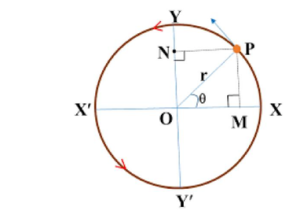
In ΔOMP,

or, y=rSinθ,  where, θ = ωt
or, y=rSinωt……….………. 1)
This equation (1) is the displacement equation for simple harmonic motion.
NOTE:

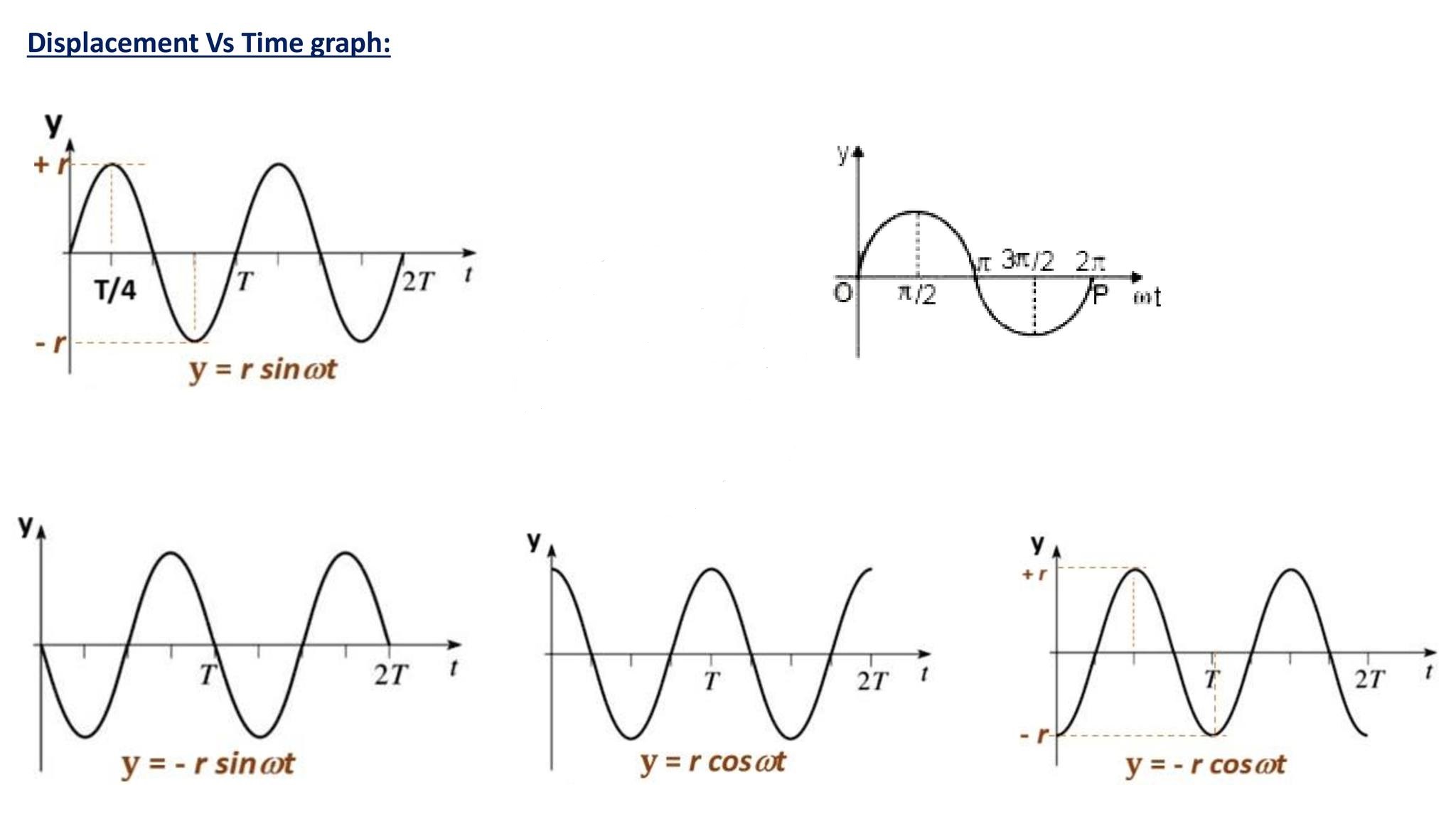
→ If the particle is at mean position i.e. y = 0 at t = 0, then the general equation of SHM is
y = r sinωt
→ If the particle is not at mean position at t = 0, then the general equation of SHM is
y = r sin(ωt±∅)
→ If the particle is at extreme position i.e. y = r at t = 0, then the general equation of SHM is
y=rcos⁡ωt

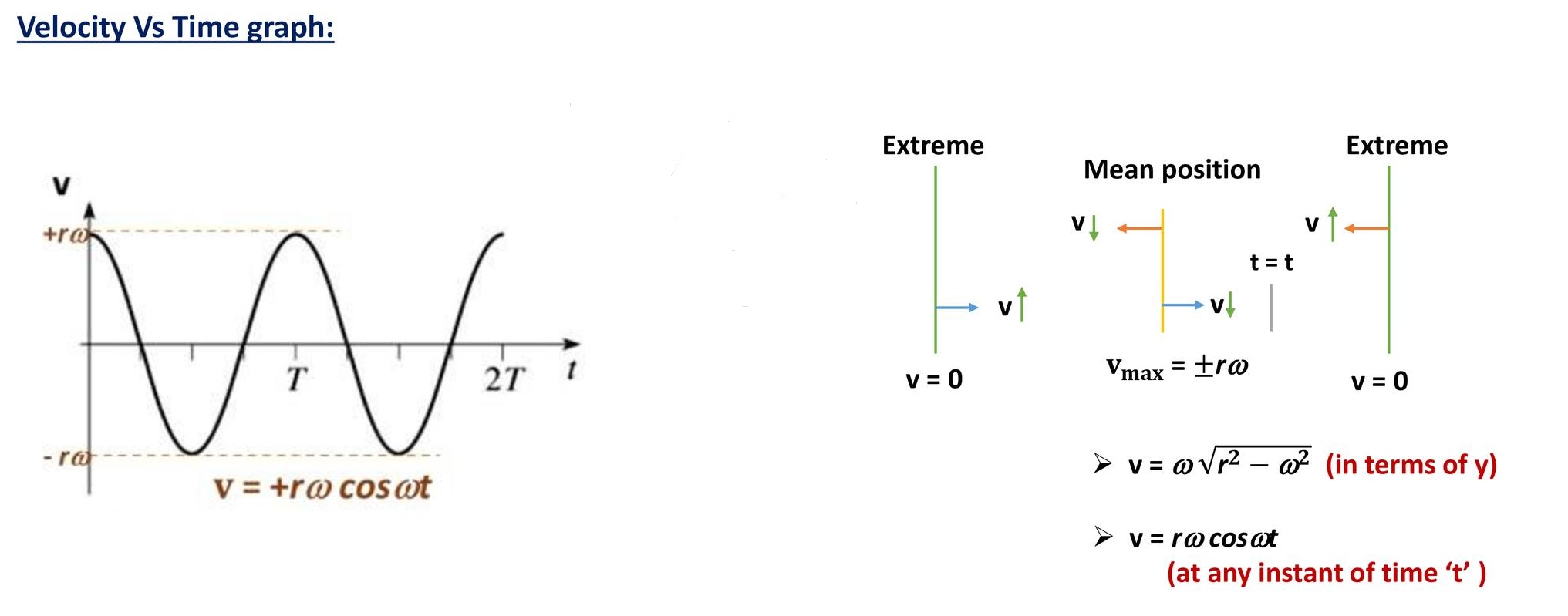
b) Velocity in SHM:

The rate of change of displacement of the particle gives velocity.

Cases:

i) At mean position, y=0
∴ $r\omega$ (max) i.e., at the mean position, velocity is maximum.

ii) At extreme position, y=r
∴ v=0(min) i.e., at the extreme position, velocity is zero.

c) Acceleration in SHM:
The rate of change of velocity of a particle gives acceleration.

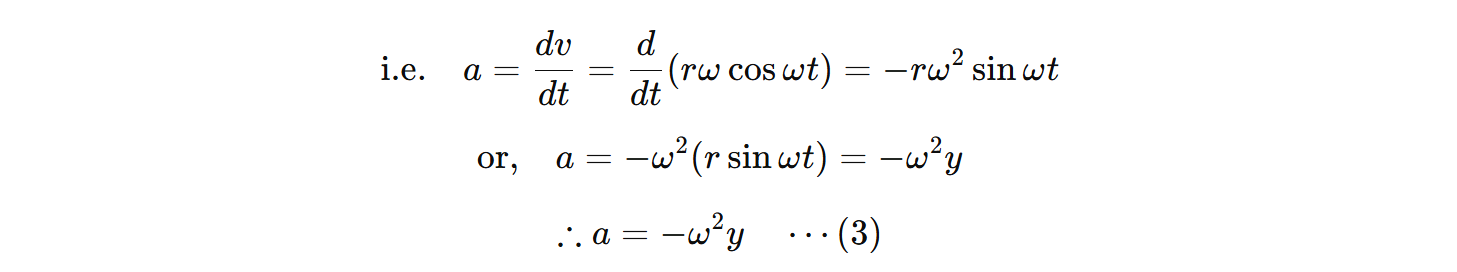
This is the expression for acceleration in SHM.

d) Amplitude:

The maximum displacement of the particle from the mean position is called amplitude. Its SI unit is metre.
The expression of the particle executing SHM is

$y=r\sin \omega t$.

When sin⁡ωt=1, y  will be maximum, therefore ,y(max)​=r. So, r is the amplitude of the particle executing SHM.

e) Time period:

Time taken by a particle in SHM to complete its one oscillation is called time period. It is denoted by T. Its SI unit is second. It is given by the relation,

T=2π/ω

f) Frequency:

The number of complete oscillations made by a particle in one second is called frequency of oscillation of the particle. If f is the frequency of oscillation of the particle executing SHM, then

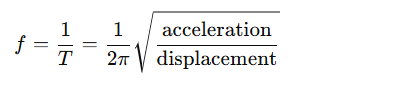
Its SI unit is cycle/second or Hertz (Hz).

​​

g) Phase:

Phase is the angle which specifies the displacement and direction of motion of the point executing SHM. In the displacement equation

y=rsin⁡ωt

$\theta =\omega t$ is called phase angle of the particle in SHM.

Simple Pendulum:

A simple pendulum is a heavy metallic bob suspended by a weightless, inextensible string with frictionless rigid support that can vibrate about a fixed point. The length between the point of suspension and the center of gravity (CG) of the bob is called the effective length of the pendulum.

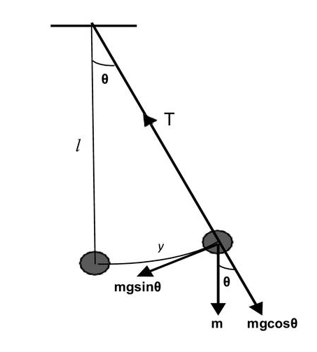
Consider a simple pendulum having the mass of the bob m and an effective length l. Let the pendulum be slightly displaced from its mean position through small angular displacement θ and the corresponding arc length y. In the displaced position, the weight mg of the bob can be resolved into two components.

• The component mgcosθ balances the tension T in the string.
• The component mgsinθ tends to bring the bob into the mean position and hence acts as a restoring force.

Second Pendulum:

A simple pendulum whose time period is two second is called second pendulum. i.e. T = 2 sec.

On the earth’s surface, g = 9.8 m/s² and from the relation,

Mass spring system:

1. Horizontal oscillation of mass spring system:

Consider a body of mass m is connected to one end of a spring whose another end is connected to a fixed rigid wall and the mass is placed on a smooth (frictionless) horizontal surface as shown in figure. Let the mass be slightly pulled outward so that an extension y is produced in the spring. According to Hooke’s law, the restoring force acting on the mass is given by,

F ∝ y

or,  F= – ky ……….(1)

Where k is the force constant and the negative sign indicates that the restoring force acts in the opposite direction of displacement of the body from the mean position.

When the pulled mass is released, it executes oscillation about the mean position. If a be the acceleration produced, then

ma = -ky

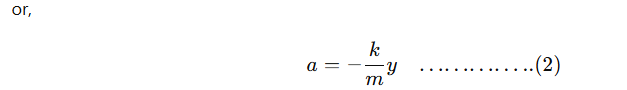
Since k and m are constant

a  ∝   −y

Hence, the horizontal oscillation of mass spring system executes simple harmonic motion.

For simple harmonic motion, we have,
Thus, the time period of horizontal oscillation of a mass-spring system depends upon the mass of the body and the force constant of the spring.

2. Vertical oscillation of mass spring system: (Helical spring system)

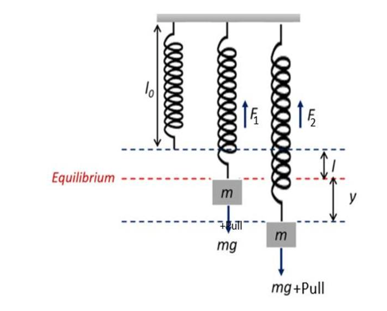
Consider a spring suspended vertically on a fixed rigid support. Let a mass m be attached at the lower end of a spring so that an extension l is produced in the spring. This is the equilibrium position of the mass-spring system (i.e., mass is at rest). The restoring force acting on the mass is given by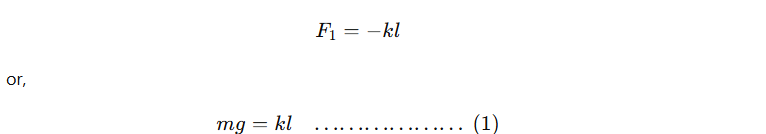

where k is the force constant or spring constant of the spring. The negative sign shows that the force opposes the displacement from the mean position.

Let the mass be further pulled downward through a distance y. Then the new restoring force produced in the spring is given by
When the mass is released, it moves to and from about the equilibrium position. The net force that causes the oscillation of the mass is (when the mass moves upward):

When the mass is released, it moves to and from about the equilibrium position. The net force that causes the oscillation of the mass is (when the mass moves upward):

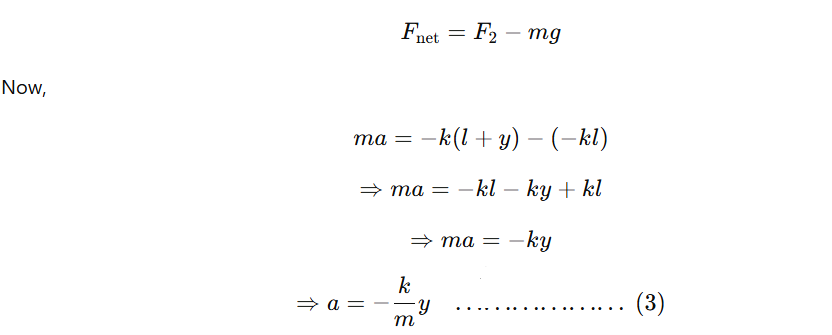
Since k and mmm are constants,

a  ∝−y

Hence, the vertical oscillation of the mass-spring system executes Simple Harmonic Motion (S.H.M.).

Energy in SHM:

A particle executing SHM has both kinetic and potential energy. So, the total energy of a particle in SHM is equal to the sum of its kinetic and potential energy.

Kinetic Energy in SHM:
Velocity in SHM is given by the relation,

where,
ω = angular frequency,
r = amplitude,
y= displacement from the mean position.

∴ The kinetic energy (K.E.) of a particle with mass m in SHM is given by

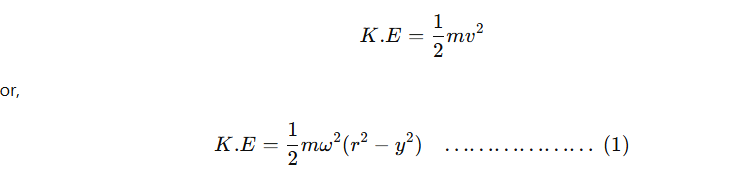
Potential energy in SHM:

Acceleration in SHM is given by

a=−ω²y

where, $\omega$ is angular frequency; $r$ is amplitude and $y$ is displacement from mean position. The restoring force acting on the particle is given by,

      F=ma=−mω²y

or,  F =  – ky 

Where, k= mω² is a constant called force constant of SHM. Now, small amount of work done in displacing the particle by a small displacement ‘dy’ against the restoring force is given by, 

dW=−Fdy

Negative sign shows that the work is done against the restoring force.

dW=kydy…(2)

The total amount of work done in displacing the particle from mean position to displacement y is

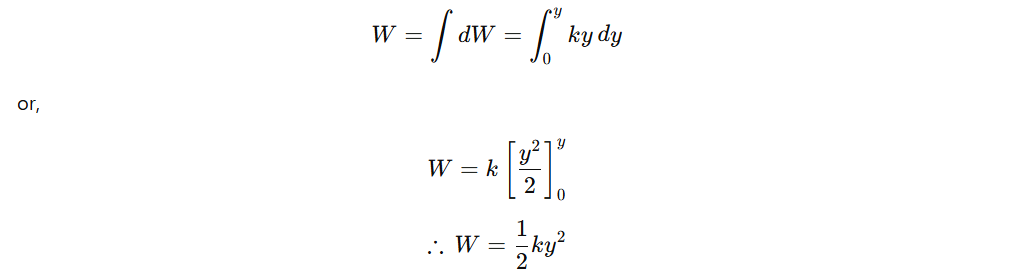
This amount of work done is stored in the particle in the form of potential energy. i.e.

Now total energy of the particle in SHM is given by,

E=K.E+P.E 

or,  

As $,\omega$ and $r$ are constants, the total energy remains constant for a particle executing SHM.

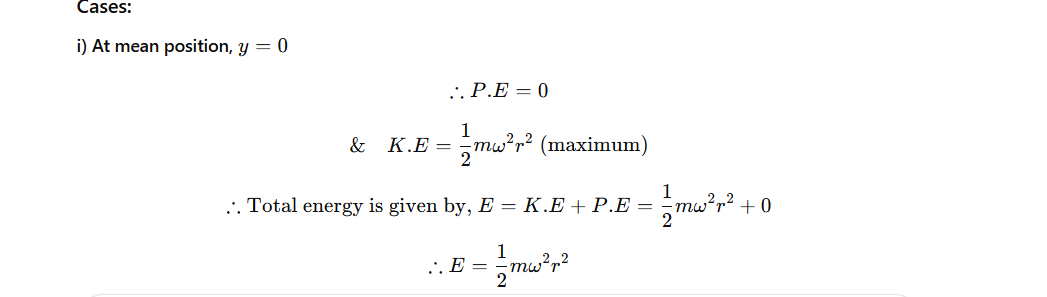
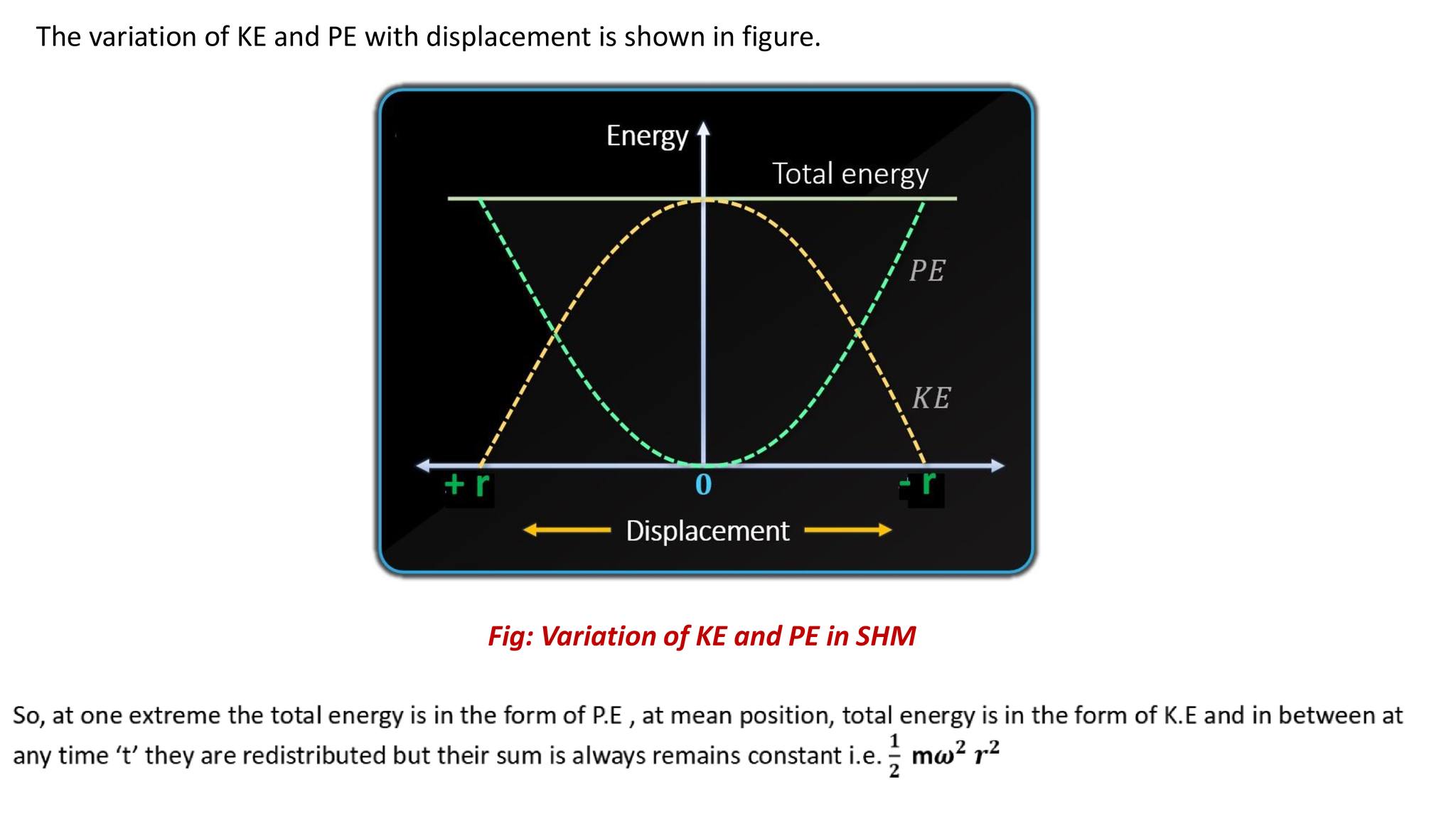
Thus, total energy remains conserved in simple harmonic motion.

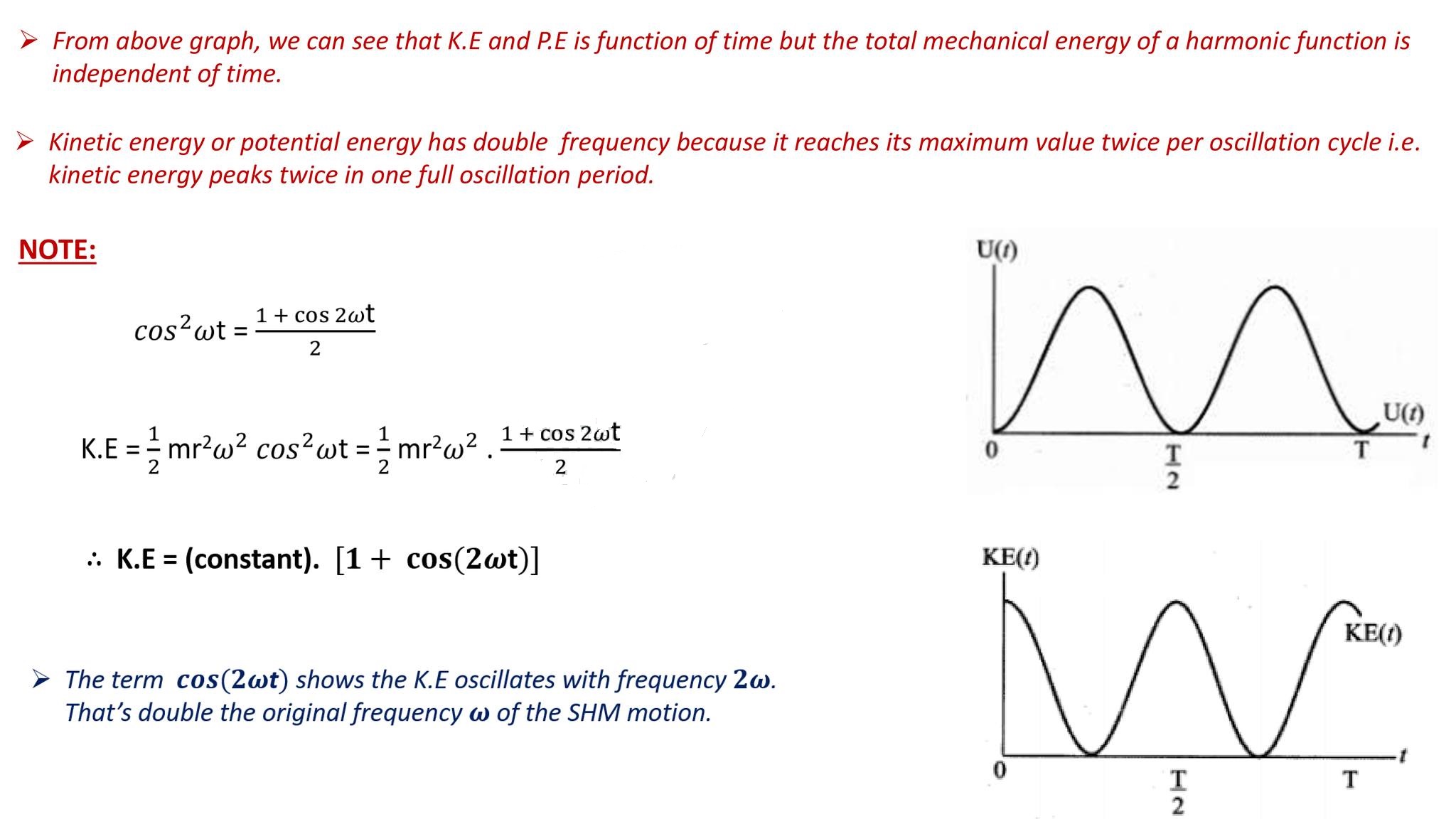
Angular simple harmonic motion:

The periodic motion in which a body rotates back and forth such that the angular acceleration is directly proportional to the angular displacement from mean position and opposes the angular displacement from mean position is called angular simple harmonic motion. i.e. for angular SHM,

α ∝−θ

where θ is the angular displacement from mean position. The negative sign shows that the acceleration opposes the displacement from mean position. Similar to linear SHM, equation of angular SHM is given by,

θ=θ₀​sin(ωt+ϕ)

where ϕ is the initial phase angle and θ0​ is the maximum angular displacement from mean position called angular amplitude.

Torsional pendulum:

A torsional pendulum consists of a circular disc suspended horizontally on a rigid support about its center of gravity with the help of a wire. Suppose the disc is slightly rotated from its mean position through small angular displacement θ so that a torsion or twist is produced in the suspension wire.

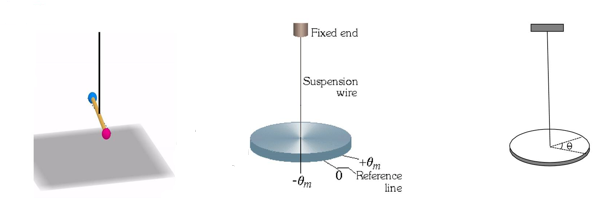
Due to torsion or twist in the suspension wire, a restoring torque acts on the disc which is directly proportional to the angular displacement (or twisting angle).

$$\text{.}\tau \propto \theta$$

or, τ=−cθ………………(1)

where $c$ is a constant known as the torsional constant of the wire.

Compiled By Er. Basant Kumar Yadav